Write Up 2: Exploring The Parabola

Introduction:

For this assignment. we will be exploring parabolas and their mathematical characteristics; specifically the quadratic. Throughout this exploration, we will look at translations, vertical shifts, horizontal shifts, and dilations of parabolas. We will first observe the graph of our function .

Exploration Part 1: Parabolic Characterics

Lets observe some characteristics of the parabola . The vertex can be found using the common vertex formula [b/2a, f(-b/2a)]. For our specific parabola, the vertex is (-0.75,-5.125).

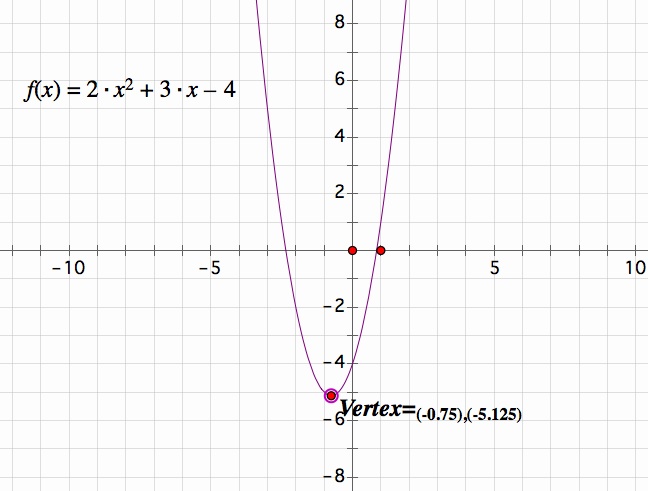
We can also observe the stretch or compress of this parabola is determined by the "2" in our function .

Another similar characteristic to most other functions is the y-intercept, which in this case is -4. We can observe below how the y-intercept varies on vertical shift of the graph:

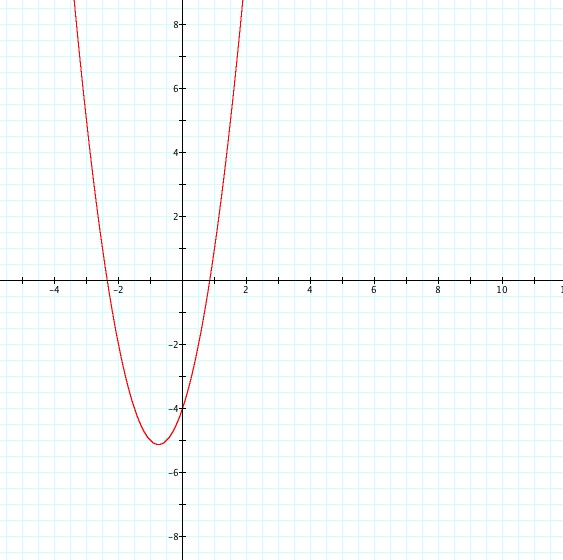
Let's also observe below exactly what happens when our variable "b=3" varies in our parabola . The vertex of our parabola follows the the path of the parabola .

Exploration Part i: Overlay a new graph relaxing each x with (x-4)

                                    Old graph of                                        New Graph of

                         

---

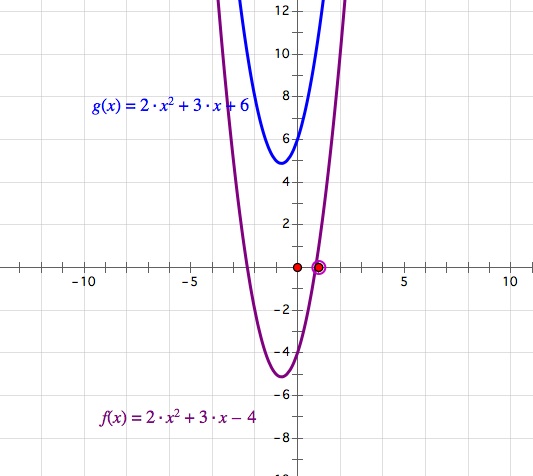
Now let's take a look at a Cartesian plot with both of our functions on the same set of axes:

By replacing each x with a (x-4), the vertex of our original parabola shift to the right 4 units as seen by the horizontal blue line. This makes sense because the vertical shift of a graph occurs when some constant is added or subtracted to the variable x in the graphs equation. We can find the value of a horizontal shift by solving inside the parentheses for the variable x. In this part of the exploration, we replace each x with an (x-4) and by solving for the x in the parentheses we get x-4=0. Therefore, x=4 which means that our horizontal shift that occurs from our original equation is shifted four positive units to the right seen in the above graph.

Exploration Part (ii): Change the equation to move the vertex of the graph into the second quadrant

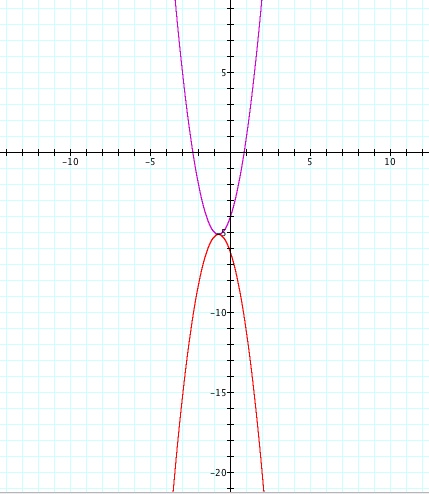
Lets observe that the only difference in these two graphs is the vertical shift component of their equations. Lets observe that the constant in the parabolic equation gives us the value of the y-intercept of the graph. Therefore in order to move our original graph, which is represented by the purple graph, into the 2nd quadrant we need to change the value of the y-intercept in our parabolic equation to move our vertex. Since the only thing changing in our equations in the constant or y-intercept, the x component of the vertex does not change which restricts our vertex to the 2nd or 4th quadrants. Also we know that our original graph's vertex lies in the fourth quadrant, therefore in order to move our vertex into the 2nd quadrant have to adjust the vertical shift of the graph. We can do this by forcing our constant to approximately greater than (11/10) which gives us a y-value in our vertex greater than 0.

Exploration Part (iii): Change the equation to produce a graph concave down that shares the same vertex

We have to understand that in order for these two graphs to share the same vertex, the x and y    components of the vertex must be the same. Therefore the x component must be equal to -.75 and the y component must equal -5.125. Let's observe that in order for our graph to become concave down the constant "a" in the general parabolic formula must be negative.  Again, the parabolic equation must have the x-component of the vertex to be -0.75 and we find the x-component of the vertex by (-b/2a). Therefore if the sign of the constant "a" changes to make the graph concave down, so must the sign for the constant "b" in to keep our x-component of the vertex the same at -0.75. If the signs of the constants "a" and "b" are opposite from our original equation, then we get the equation . The only thing wrong with our new equation is that the constant "c=4" will not allow for the vertex to be the same as the vertex for . In order to find the appropriate constant "c" which gives us the same vertex, we must use some algebra. We know from our original equation that the y-component of the vertex must equal -5.125. Therefore we can plug in our x-component value of -0.75 into the equation which gives us . Now we can solve for "c" which gives us c= -6.25. Hence our new equation of the graph which is concave down and shares the same vertex as is the equation .

 

 

---

Exploration Part iv: Generalize

   First, in order to flip a parabola we must reverse the sign of the constant "a" in our general parabolic equation .

   The y-intercept of the parabola is given by the constant "c" in our general parabolic equation

   We can horizontally shift a parabolic graph by adding or subtracting a constant to our variable x. For example   => 

   We can vertically shift our graph by varying the constant "c" in our general parabolic equation